partynsa.blogg.se - Standard error microsoft excel data analysis regression

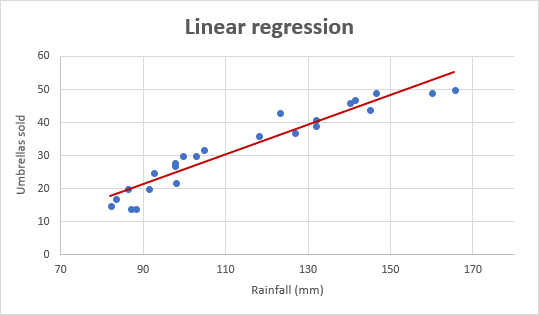
That sounds a lot faster! However, it makes a huge difference whether the initial speed was 20 MPH or 90 MPH. R-squared is equivalent to saying that the car went 80% faster. Suppose we’re talking about how fast a car is traveling.Įxample Regression Model: BMI and Body Fat Percentage

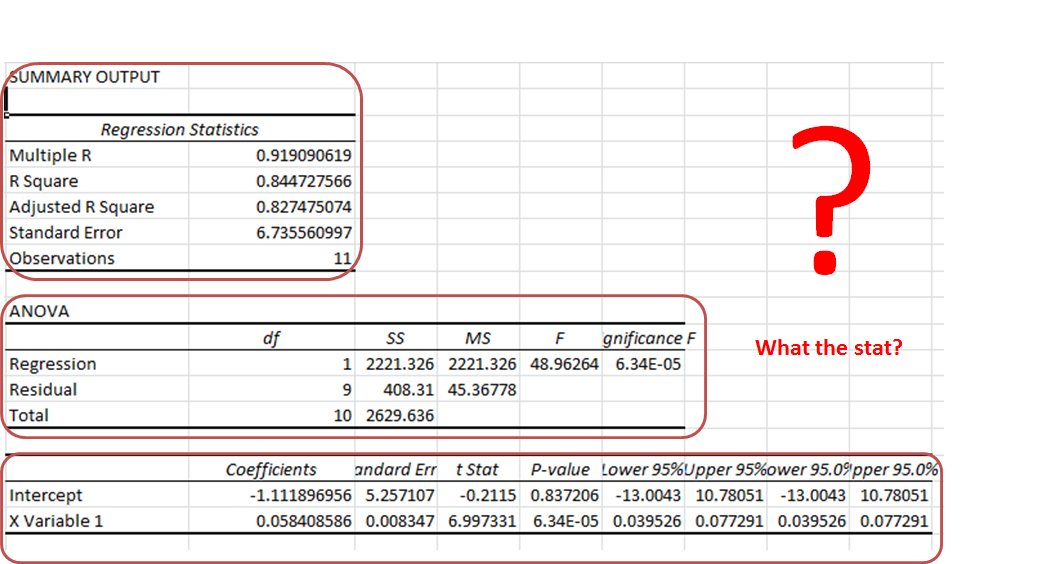
R-squared can range from 0 to 100%.Īn analogy makes the difference very clear. R-squared provides the relative measure of the percentage of the dependent variable variance that the model explains.S is in the units of the dependent variable. The standard error of the regression provides the absolute measure of the typical distance that the data points fall from the regression line.However, there are differences between the two statistics. Both of these measures give you a numeric assessment of how well a model fits the sample data. You can find the standard error of the regression, also known as the standard error of the estimate, near R-squared in the goodness-of-fit section of most statistical output. At the very least, you’ll find that the standard error of the regression is a great tool to add to your statistical toolkit!Ĭomparison of R-squared to the Standard Error of the Regression (S)Īs R-squared increases and S decreases, the data points move closer to the line I think you’ll see that the oft overlooked standard error of the regression can tell you things that the high and mighty R-squared simply can’t. We’ll also work through a regression example to help make the comparison. Other than that, I have not had to use any other quantity on the regression statistics table in my 7 University semesters.In this post, I’ll compare these two statistics.

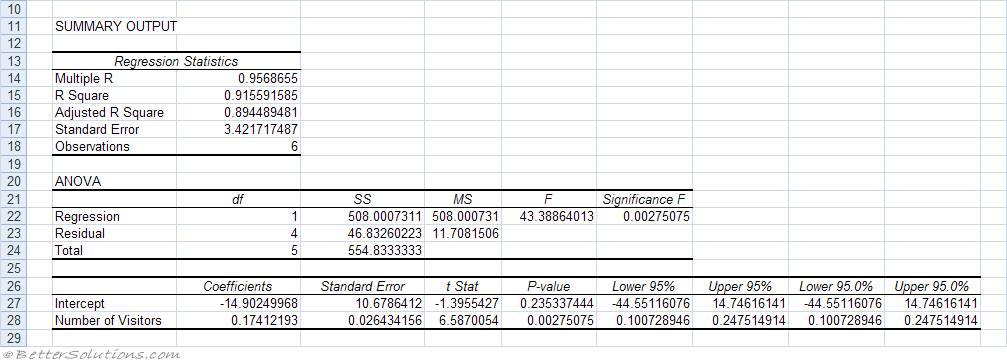
The closer it is to #1#, the better it is, but it is only for a linear fit line. Oftentimes, even in a quantitative analysis course, you only need to further know the coefficient of determination #R^2#. Here is an example of an Ohm's law analysis I did using a similar regression statistics table: Where #s# is the standard deviation above, and: Where #N# is the number of trials, #x_i# is each individual value, and #barx# is the average of said values.

Intercept Associated Error ( #AE_"int"#).

The Associated Error is basically the uncertainty you have.įor example, in a standard physics lab course, bare minimum, here's what you would need to know: If you multiply the Standard Error by #1.96#, you get the Associated Error for either the Intercept or the Slope. "HH SIZE" refers to the Slope, and of course, Intercept is the y-intercept. The "Coefficients" are the slope or y-intercept in this case.